刷题笔记:[2021江西省赛]ez rsa

前言

基友发的题，不难，但小有门槛，很值得一做。

题目给出了n,e,c,p-q

• n

  27552304606229034903366058815849954030287648695063385362955432137790872571412035824128918674719247737295565001575991597519270789776408208970323808016733976338433371328100880898942106515627607388226912870981180215883273805491209461671730377099185278711453949265641966582563910708529619185885928310168288810488784242368160743359666583499117949407921812317700250240067929572558785431071173411100434109661677786734923283679392823901052633992456780285091988542875991410528415886437666510014123352497264017734716859350294159440761760921548702546470902740121962033241003215821780125194400741190925169397917247376657863011603

• e

  65537

• c

  8643831704675414121804983915084443744489969712473300784256427784417167322852556975560503484179280700293119974607254037642425650493676448134024809335297135239994950178868535219541095694358323044214971760829173918774094415933808417722001811285178546917655837402000771685507972240389565704149610032767242977174132826100177368764169367458684152505611469248099487912367364804360878611296860803835816266114046682291529593099394952245852157119233687981777202751472502060481232341206366584532964027749320641690448228420342308891797513656897566100268729012788419021059054907653832828437666012596894150751431936476816983845357

• p-q

  3216514606297172806828066063738105740383963382396892688569683235383985567043193404185955880509592930874764682428425994713750665248099953457550673860782324431970917492727256948066013701406000049963109681898567026552657377599263519201715733179565306750754520746601394738797021362510415215113118083969304423858

题解

已知：

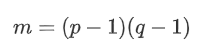
然后配凑一下

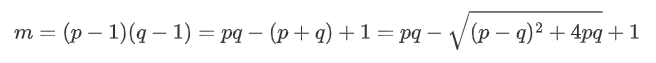
已知n=pq和p-q，所以可以在不算出p/q单个值的情况下直接算出m。算出m之后就是常规的rsa解法。

但问题来了，数字那么大，该怎么算？

掏出segamath

t是p-q

n = 27552304606229034903366058815849954030287648695063385362955432137790872571412035824128918674719247737295565001575991597519270789776408208970323808016733976338433371328100880898942106515627607388226912870981180215883273805491209461671730377099185278711453949265641966582563910708529619185885928310168288810488784242368160743359666583499117949407921812317700250240067929572558785431071173411100434109661677786734923283679392823901052633992456780285091988542875991410528415886437666510014123352497264017734716859350294159440761760921548702546470902740121962033241003215821780125194400741190925169397917247376657863011603
t = 3216514606297172806828066063738105740383963382396892688569683235383985567043193404185955880509592930874764682428425994713750665248099953457550673860782324431970917492727256948066013701406000049963109681898567026552657377599263519201715733179565306750754520746601394738797021362510415215113118083969304423858
m = n-(t*t+4*n).sqrt()+1
print(m)

算出m：

27552304606229034903366058815849954030287648695063385362955432137790872571412035824128918674719247737295565001575991597519270789776408208970323808016733976338433371328100880898942106515627607388226912870981180215883273805491209461671730377099185278711453949265641966582563910708529619185885928310168288810488452249048361792190062286900087513922744159737091583808351713622260845711638281055969511895420947879300731919183830759012447400161458551140739059886287572056575864045508330251848028360471591770162350542916982579543446708446143640478066426347229913784237231663261383992631285889273004630202243388356152746024080

普通python环境下会报错的。

在segamath就可以跑。我原以为segamath仅仅是python库，调用其方法才能体现它的特别之处，但没想到它是把python内部都给改造成了合适的形状，可以直接进行大数计算，十分舒服！

然后就是rsa常规解法。

先求d，d是e在模m下的逆元：d*e%m=1

再求明文plain，plain=c^d%n

这里使用gmpy2，主要是segamath不知道怎么求模逆元。

import gmpy2 as gp
import binascii
c = 8643831704675414121804983915084443744489969712473300784256427784417167322852556975560503484179280700293119974607254037642425650493676448134024809335297135239994950178868535219541095694358323044214971760829173918774094415933808417722001811285178546917655837402000771685507972240389565704149610032767242977174132826100177368764169367458684152505611469248099487912367364804360878611296860803835816266114046682291529593099394952245852157119233687981777202751472502060481232341206366584532964027749320641690448228420342308891797513656897566100268729012788419021059054907653832828437666012596894150751431936476816983845357
e = 65537
m = 27552304606229034903366058815849954030287648695063385362955432137790872571412035824128918674719247737295565001575991597519270789776408208970323808016733976338433371328100880898942106515627607388226912870981180215883273805491209461671730377099185278711453949265641966582563910708529619185885928310168288810488452249048361792190062286900087513922744159737091583808351713622260845711638281055969511895420947879300731919183830759012447400161458551140739059886287572056575864045508330251848028360471591770162350542916982579543446708446143640478066426347229913784237231663261383992631285889273004630202243388356152746024080
n = 27552304606229034903366058815849954030287648695063385362955432137790872571412035824128918674719247737295565001575991597519270789776408208970323808016733976338433371328100880898942106515627607388226912870981180215883273805491209461671730377099185278711453949265641966582563910708529619185885928310168288810488784242368160743359666583499117949407921812317700250240067929572558785431071173411100434109661677786734923283679392823901052633992456780285091988542875991410528415886437666510014123352497264017734716859350294159440761760921548702546470902740121962033241003215821780125194400741190925169397917247376657863011603
d = gp.invert(e, m)
plain = pow(c, d, n)
print(plain)  # 算出的是10进制数
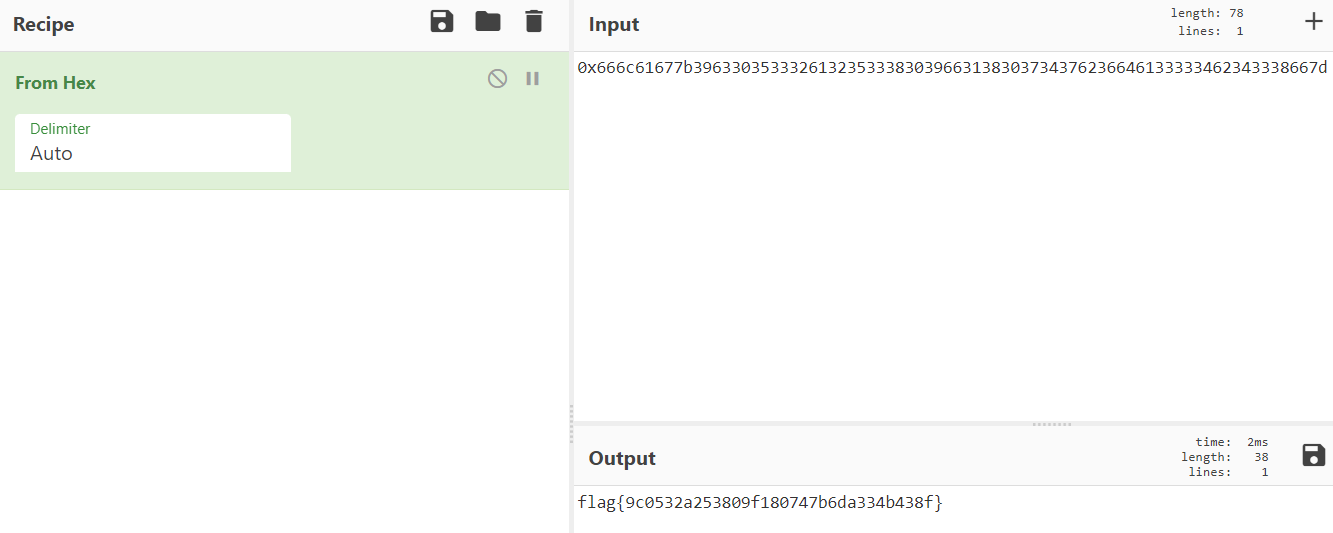
print(hex(plain))  # 将该十进制数转换为16进制数

最后